SnowFlake算法生成全局唯一ID

“有这么一种说法，自然界中并不存在两片完全一样的雪花的。每一片雪花都拥有自己漂亮独特的形状、独一无二。”

有时候在等快递，想着刚买的火锅底料什么时候会到，就用那一长串的订单编号，去查询物流。在这过程中，我会想到(其实也没有)，订单编号是怎么在一个巨大的商城中保持唯一性的？

在我做一个开始制作一个订单表的时候，思考过订单编号这个问题，如果我每够买一个商品，下完单付款之后，就会在订单表写入商品信息和订单编号，那么这个时候订单的编号必定要全局唯一，想到全局唯一，那么我在前一个订单的订单编号上+1，保持这个订单编号的原子性，那不就好了？

但是也会诞生一个问题，比如你的订单编号一直都是以1、2、3、4、5、6这样的方式增长的话，那么别人也很容易猜到你当前的订单编号，而且如果把它作为一个奖券编号的话，那就很没逻辑性了。

所以，我想引入时间戳的方式，拼串，诞生一个全局唯一的ID，不过偶然间看到了Twitter上的雪花算法，便觉得很有意思，于是乎便拿来使用了。

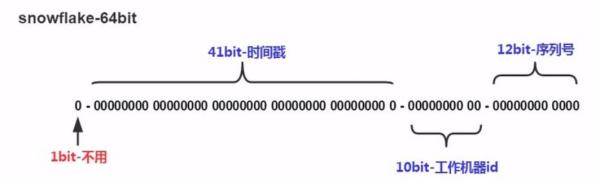
雪花算法

雪花算法并不复杂，它的本体是一个64bit：

组成结构：

1位，不用。二进制中最高位为1的都是负数，但是我们生成的id一般都使用整数，所以这个最高位固定是0
41位，用来记录时间戳（毫秒）。
- 41位可以表示个数字，
- 如果只用来表示正整数（计算机中正数包含0），可以表示的数值范围是：0 至，减1是因为可表示的数值范围是从0开始算的，而不是1。
- 也就是说41位可以表示个毫秒的值，转化成单位年则是年
10位，用来记录工作机器id。
- 可以部署在个节点，包括5位datacenterId和5位workerId
- 5位（bit）可以表示的最大正整数是，即可以用0、1、2、3、….31这32个数字，来表示不同的datecenterId或workerId
12位，序列号，用来记录同毫秒内产生的不同id。
- 12位（bit）可以表示的最大正整数是，即可以用0、1、2、3、….4094这4095个数字，来表示同一机器同一时间截（毫秒)内产生的4095个ID序号

SnowFlake可以保证：

所有生成的id按时间趋势递增
整个分布式系统内不会产生重复id

源码

标上了注释，后面会单独挑几个出来仔细说明

/**
 * Twitter_Snowflake
 * SnowFlake的结构如下(每部分用-分开):
 * 0 - 0000000000 0000000000 0000000000 0000000000 0 - 00000 - 00000 - 000000000000 <br>
 * SnowFlake的优点是，整体上按照时间自增排序，并且整个分布式系统内不会产生ID碰撞(由数据中心ID和机器ID作区分)
 */
public class IdWorker {

    /** 开始时间截 (2015-01-01) */
    private final long twepoch = 1420041600000L;

    /** 机器id所占的位数 */
    private final long workerIdBits = 5L;

    /** 数据标识id所占的位数 */
    private final long datacenterIdBits = 5L;

    /** 支持的最大机器id，结果是31 (这个移位算法可以很快的计算出几位二进制数所能表示的最大十进制数) */
    private final long maxWorkerId = -1L ^ (-1L << workerIdBits);

    /** 支持的最大数据标识id，结果是31 */
    private final long maxDatacenterId = -1L ^ (-1L << datacenterIdBits);

    /** 序列在id中占的位数 */
    private final long sequenceBits = 12L;

    /** 机器ID向左移12位 */
    private final long workerIdShift = sequenceBits;

    /** 数据标识id向左移17位(12+5) */
    private final long datacenterIdShift = sequenceBits + workerIdBits;

    /** 时间截向左移22位(5+5+12) */
    private final long timestampLeftShift = sequenceBits + workerIdBits + datacenterIdBits;

    /** 生成序列的掩码，这里为4095 (0b111111111111=0xfff=4095) */
    private final long sequenceMask = -1L ^ (-1L << sequenceBits);

    /** 工作机器ID(0~31) */
    private long workerId;

    /** 数据中心ID(0~31) */
    private long datacenterId;

    /** 毫秒内序列(0~4095) */
    private long sequence = 0L;

    /** 上次生成ID的时间截 */
    private long lastTimestamp = -1L;


    /**
     * 构造函数
     * @param workerId 工作ID (0~31)
     * @param datacenterId 数据中心ID (0~31)
     */
    public IdWorker(long workerId, long datacenterId) {
        if (workerId > maxWorkerId || workerId < 0) {
            throw new IllegalArgumentException(String.format("worker Id can't be greater than %d or less than 0", maxWorkerId));
        }
        if (datacenterId > maxDatacenterId || datacenterId < 0) {
            throw new IllegalArgumentException(String.format("datacenter Id can't be greater than %d or less than 0", maxDatacenterId));
        }
        this.workerId = workerId;
        this.datacenterId = datacenterId;
    }

    /**
     * 获得下一个ID (该方法是线程安全的)
     * @return SnowflakeId
     */
    public synchronized long nextId() {
        long timestamp = timeGen();

        //如果当前时间小于上一次ID生成的时间戳，说明系统时钟回退过这个时候应当抛出异常
        if (timestamp < lastTimestamp) {
            throw new RuntimeException(
                    String.format("Clock moved backwards.  Refusing to generate id for %d milliseconds", lastTimestamp - timestamp));
        }

        //如果是同一时间生成的，则进行毫秒内序列
        if (lastTimestamp == timestamp) {
            sequence = (sequence + 1) & sequenceMask;
            //毫秒内序列溢出
            if (sequence == 0) {
                //阻塞到下一个毫秒,获得新的时间戳
                timestamp = tilNextMillis(lastTimestamp);
            }
        }
        //时间戳改变，毫秒内序列重置
        else {
            sequence = 0L;
        }

        //上次生成ID的时间截
        lastTimestamp = timestamp;

        //移位并通过或运算拼到一起组成64位的ID
        return ((timestamp - twepoch) << timestampLeftShift) //
                | (datacenterId << datacenterIdShift) //
                | (workerId << workerIdShift) //
                | sequence;
    }

    /**
     * 阻塞到下一个毫秒，直到获得新的时间戳
     * @param lastTimestamp 上次生成ID的时间截
     * @return 当前时间戳
     */
    protected long tilNextMillis(long lastTimestamp) {
        long timestamp = timeGen();
        while (timestamp <= lastTimestamp) {
            timestamp = timeGen();
        }
        return timestamp;
    }

    /**
     * 返回以毫秒为单位的当前时间
     * @return 当前时间(毫秒)
     */
    protected long timeGen() {
        return System.currentTimeMillis();
    }
}

代码理解

上面大部分代码都是比较易读的，但是有一些涉及到了位运算的代码，单独拿出来说说，这到底是为什么。

负数的二进制

在计算机中，负数的二进制是用补码来表示的。

假设我是用Java中的int类型来存储数字的，int类型的大小是32个二进制位（bit），即4个字节（byte）。（1 byte = 8 bit），那么十进制数字3在二进制中的表示应该是这样的：

1 2	00000000 00000000 00000000 00000011 // 3的二进制表示，就是原码

那数字-3在二进制中应该如何表示？

我们可以反过来想想，因为-3+3=0，在二进制运算中把-3的二进制看成未知数x来求解，
求解算式的二进制表示如下：

 
   00000000 00000000 00000000 00000011 //3，原码
+  xxxxxxxx xxxxxxxx xxxxxxxx xxxxxxxx //-3，补码
-----------------------------------------------
   00000000 00000000 00000000 00000000

反推x的值，3的二进制加上什么值才使结果变成：00000000 00000000 00000000 00000000？

   00000000 00000000 00000000 00000011 //3，原码                         
+  11111111 11111111 11111111 11111101 //-3，补码
-----------------------------------------------
 1 00000000 00000000 00000000 00000000

反推的思路是3的二进制数从最低位开始逐位加1，使溢出的1不断向高位溢出，直到溢出到第33位。然后由于int类型最多只能保存32个二进制位，所以最高位的1溢出了，剩下的32位就成了（十进制的）0。

补码的意义就是可以拿补码和原码（3的二进制）相加，最终加出一个“溢出的0”

以上是理解的过程，实际中记住公式就很容易算出来：

补码 = 反码 + 1
补码 = （原码 - 1）再取反码

因此-1的二进制应该这样算：

1
2
3

00000000 00000000 00000000 00000001 //原码：1的二进制
11111111 11111111 11111111 11111110 //取反码：1的二进制的反码
11111111 11111111 11111111 11111111 //加1：-1的二进制表示（补码）

用位运算计算n个bit能表示的最大数值

比如这样一行代码：

1 2	private long workerIdBits = 5L; private long maxWorkerId = -1L ^ (-1L << workerIdBits);

上面代码换成这样看方便一点：

1	long maxWorkerId = -1L ^ (-1L << 5L)

上面那行代码中，运行顺序是：

-1 左移 5，得结果a
-1 异或 a

long maxWorkerId = -1L ^ (-1L << 5L)的二进制运算过程如下：

-1 左移 5，得结果a ：

1
2
3

      11111111 11111111 11111111 11111111 //-1的二进制表示（补码）
11111 11111111 11111111 11111111 11100000 //高位溢出的不要，低位补0
      11111111 11111111 11111111 11100000 //结果a

-1 异或 a ：

        11111111 11111111 11111111 11111111 //-1的二进制表示（补码）
    ^   11111111 11111111 11111111 11100000 //两个操作数的位中，相同则为0，不同则为1
---------------------------------------------------------------------------
        00000000 00000000 00000000 00011111 //最终结果31

最终结果是31。

那既然现在知道算出来long maxWorkerId = -1L ^ (-1L << 5L)中的maxWorkerId = 31，有什么含义？为什么要用左移5来算？如果你看过概述部分，请找到这段内容看看：

5位（bit）可以表示的最大正整数是，即可以用0、1、2、3、….31这32个数字，来表示不同的datecenterId或workerId。

-1L ^ (-1L << 5L)结果是31，的结果也是31，所以在代码中，-1L ^ (-1L << 5L)的写法是利用位运算计算出5位能表示的最大正整数是多少

用mask防止溢出

还有一段这样的代码：

1	sequence = (sequence + 1) & sequenceMask;

分别用不同的值测试一下，你就知道它怎么有趣了：

long seqMask = -1L ^ (-1L << 12L); //计算12位能耐存储的最大正整数，相当于：2^12-1 = 4095
        System.out.println("seqMask: "+seqMask);
        System.out.println(1L & seqMask);
        System.out.println(2L & seqMask);
        System.out.println(3L & seqMask);
        System.out.println(4L & seqMask);
        System.out.println(4095L & seqMask);
        System.out.println(4096L & seqMask);
        System.out.println(4097L & seqMask);
        System.out.println(4098L & seqMask);
 
        
/*
        seqMask: 4095
        1
        2
        3
        4
        4095
        0
        1
        2
*/

这段代码通过位与运算保证计算的结果范围始终是 0-4095 ！

这代表着它在一毫秒内生成ID的上限值就是4096个，如果超过这个值，则会阻塞至下一个毫秒。

用位运算汇总结果

还有另外一段诡异的代码：

return ((timestamp - twepoch) << timestampLeftShift) |
        (datacenterId << datacenterIdShift) |
        (workerId << workerIdShift) |
        sequence;

为了弄清楚这段代码，首先需要计算一下相关的值：

private long twepoch = 1288834974657L; //起始时间戳，用于用当前时间戳减去这个时间戳，算出偏移量
 
private long workerIdBits = 5L; //workerId占用的位数：5
private long datacenterIdBits = 5L; //datacenterId占用的位数：5
private long maxWorkerId = -1L ^ (-1L << workerIdBits);  // workerId可以使用的最大数值：31
private long maxDatacenterId = -1L ^ (-1L << datacenterIdBits); // datacenterId可以使用的最大数值：31
private long sequenceBits = 12L;//序列号占用的位数：12
 
private long workerIdShift = sequenceBits; // 12
private long datacenterIdShift = sequenceBits + workerIdBits; // 12+5 = 17
private long timestampLeftShift = sequenceBits + workerIdBits + datacenterIdBits; // 12+5+5 = 22
private long sequenceMask = -1L ^ (-1L << sequenceBits);//4095
 
private long lastTimestamp = -1L;

其次写个测试，把参数都写死，并运行打印信息，方便后面来核对计算结果：

 
//---------------测试---------------
public static void main(String[] args) {
    long timestamp = 1505914988849L;
    long twepoch = 1288834974657L;
    long datacenterId = 17L;
    long workerId = 25L;
    long sequence = 0L;
 
    System.out.printf("\ntimestamp: %d \n",timestamp);
    System.out.printf("twepoch: %d \n",twepoch);
    System.out.printf("datacenterId: %d \n",datacenterId);
    System.out.printf("workerId: %d \n",workerId);
    System.out.printf("sequence: %d \n",sequence);
    System.out.println();
    System.out.printf("(timestamp - twepoch): %d \n",(timestamp - twepoch));
    System.out.printf("((timestamp - twepoch) << 22L): %d \n",((timestamp - twepoch) << 22L));
    System.out.printf("(datacenterId << 17L): %d \n" ,(datacenterId << 17L));
    System.out.printf("(workerId << 12L): %d \n",(workerId << 12L));
    System.out.printf("sequence: %d \n",sequence);
 
    long result = ((timestamp - twepoch) << 22L) |
            (datacenterId << 17L) |
            (workerId << 12L) |
            sequence;
    System.out.println(result);
 
}
 
/** 打印信息：
    timestamp: 1505914988849 
    twepoch: 1288834974657 
    datacenterId: 17 
    workerId: 25 
    sequence: 0 
    
    (timestamp - twepoch): 217080014192 
    ((timestamp - twepoch) << 22L): 910499571845562368 
    (datacenterId << 17L): 2228224 
    (workerId << 12L): 102400 
    sequence: 0 
    910499571847892992
*/

代入位移的值得之后，就是这样：

return ((timestamp - 1288834974657) << 22) |
        (datacenterId << 17) |
        (workerId << 12) |
        sequence;

对于尚未知道的值，我们可以先看看概述中对SnowFlake结构的解释，再代入在合法范围的值，来了解计算的过程。

当然，由于我的测试代码已经把这些值写死了，那直接用这些值来手工验证计算结果即可：

long timestamp = 1505914988849L;
long twepoch = 1288834974657L;
long datacenterId = 17L;
long workerId = 25L;
long sequence = 0L;

设：timestamp  = 1505914988849，twepoch = 1288834974657
1505914988849 - 1288834974657 = 217080014192 (timestamp相对于起始时间的毫秒偏移量)，其(a)二进制左移22位计算过程如下：                                
 
                        |<--这里开始左右22位                            ‭
00000000 00000000 000000|00 00110010 10001010 11111010 00100101 01110000 // a = 217080014192
00001100 10100010 10111110 10001001 01011100 00|000000 00000000 00000000 // a左移22位后的值(la)
                                               |<--这里后面的位补0

设：datacenterId  = 17，其（b）二进制左移17位计算过程如下：
 
                   |<--这里开始左移17位    
00000000 00000000 0|0000000 ‭00000000 00000000 00000000 00000000 00010001 // b = 17
0000000‭0 00000000 00000000 00000000 00000000 0010001|0 00000000 00000000 // b左移17位后的值(lb)
                                                    |<--这里后面的位补0

设：workerId  = 25，其（c）二进制左移12位计算过程如下：
 
             |<--这里开始左移12位    
‭00000000 0000|0000 00000000 00000000 00000000 00000000 00000000 00011001‬ // c = 25
00000000 00000000 00000000 00000000 00000000 00000001 1001|0000 00000000‬ // c左移12位后的值(lc)                                                                 
                                                          |<--这里后面的位补0

1
2
3

设：sequence = 0，其二进制如下：
 
00000000 00000000 00000000 00000000 00000000 00000000 0000‭0000 00000000‬ // sequence = 0

现在知道了每个部分左移后的值(la,lb,lc)，代码可以简化成下面这样去理解：

return ((timestamp - 1288834974657) << 22) |
        (datacenterId << 17) |
        (workerId << 12) |
        sequence;
-----------------------------
           |
           |简化
          \|/
-----------------------------
return (la) |
        (lb) |
        (lc) |
        sequence;

上面的管道符号 | 在Java中也是一个位运算符。其含义是：

x的第n位和y的第n位只要有一个是1，则结果的第n位也为1，否则为0，因此，我们对四个数的位或运算如下：

 1  |                    41                        |  5  |   5  |     12      
    
   0|0001100 10100010 10111110 10001001 01011100 00|00000|0 0000|0000 00000000 //la
   0|000000‭0 00000000 00000000 00000000 00000000 00|10001|0 0000|0000 00000000 //lb
   0|0000000 00000000 00000000 00000000 00000000 00|00000|1 1001|0000 00000000 //lc
or 0|0000000 00000000 00000000 00000000 00000000 00|00000|0 0000|‭0000 00000000‬ //sequence
------------------------------------------------------------------------------------------
   0|0001100 10100010 10111110 10001001 01011100 00|10001|1 1001|‭0000 00000000‬ //结果：910499571847892992

结果计算过程：

1) 从至左列出1出现的下标（从0开始算）：

1 2	0000 1 1 00 1 0 1 000 1 0 1 0 1 1 1 1 1 0 1 000 1 00 1 0 1 0 1 1 1 0000 1 000 1 1 1 00 1‭ 0000 0000 0000 59 58 55 53 49 47 45 44 43 42 41 39 35 32 30 28 27 26 21 17 16 15 12

2) 各个下标作为2的幂数来计算，并相加：

    2^59}  : 576460752303423488
    2^58}  : 288230376151711744   
    2^55}  :  36028797018963968    
    2^53}  :   9007199254740992     
    2^49}  :    562949953421312      
    2^47}  :    140737488355328
    2^45}  :     35184372088832
    2^44}  :     17592186044416
    2^43}  :      8796093022208
    2^42}  :      4398046511104
    2^41}  :      2199023255552
    2^39}  :       549755813888
    2^35}  :        34359738368
    2^32}  :         4294967296
    2^30}  :         1073741824
    2^28}  :          268435456
    2^27}  :          134217728
    2^26}  :           67108864
    2^21}  :            2097152
    2^17}  :             131072
    2^16}  :              65536
    2^15}  :              32768
+   2^12}  :               4096
---------------------------------------- 
             910499571847892992

观察：

 1  |                    41                        |  5  |   5  |     12      
    
   0|0001100 10100010 10111110 10001001 01011100 00|     |      |              //la
   0|                                              |10001|      |              //lb
   0|                                              |     |1 1001|              //lc
or 0|                                              |     |      |‭0000 00000000‬ //sequence
------------------------------------------------------------------------------------------
   0|0001100 10100010 10111110 10001001 01011100 00|10001|1 1001|‭0000 00000000‬ //结果：910499571847892992

上面的64位我按1、41、5、5、12的位数截开了，方便观察。

纵向观察发现:
- 在41位那一段，除了la一行有值，其它行（lb、lc、sequence）都是0，（我爸其它）
- 在左起第一个5位那一段，除了lb一行有值，其它行都是0
- 在左起第二个5位那一段，除了lc一行有值，其它行都是0
- 按照这规律，如果sequence是0以外的其它值，12位那段也会有值的，其它行都是0
横向观察发现:
- 在la行，由于左移了5+5+12位，5、5、12这三段都补0了，所以la行除了41那段外，其它肯定都是0
- 同理，lb、lc、sequnece行也以此类推
- 正因为左移的操作，使四个不同的值移到了SnowFlake理论上相应的位置，然后四行做位或运算（只要有1结果就是1），就把4段的二进制数合并成一个二进制数。

左移运算是为了将数值移动到对应的段(41、5、5，12那段因为本来就在最右，因此不用左移)。

然后对每个左移后的值(la、lb、lc、sequence)做位或运算，是为了把各个短的数据合并起来，合并成一个二进制数。

最后转换成10进制，就是最终生成的id